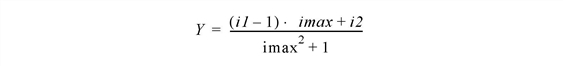
The RANDOMU function returns one or more pseudo-random numbers with one of the following distributions: uniform (the default), Gaussian, binomial, gamma, or Poisson.
Result = RANDOMU( Seed[, D1[, ..., D8]] [ [, BINOMIAL=[trials, probability]] [, /DOUBLE] [, GAMMA=integer{>0}] [, /NORMAL] [, POISSON=value] [, /UNIFORM] | [, /LONG] ] )
Returns an array of uniformly distributed random numbers of the specified dimensions.
A variable or constant used to initialize the random sequence on input, and in which the state of the random number generator is saved on output.
The state of the random number generator is contained in a long integer vector. This state is saved in the Seed argument when the argument is a named variable. To continue the pseudo-random number sequence, input the variable containing the saved state as the Seed argument in the next call to RANDOMN or RANDOMU. Each independent random number sequence should maintain its own state variable. To maintain a state over repeated calls to a procedure, the seed variable may be stored in a COMMON block.
In addition to states maintained by the user in variables, the RANDOMU and RANDOMN functions contain a single shared generic state that is used if a named variable is not supplied as the Seed argument or the named variable supplied is undefined. The generic state is initialized once using the time-of-day, and may be re-initialized by providing a Seed argument that is a constant or expression.
If the Seed argument is:
Note: RANDOMN and RANDOMU use the same sequence, so starting or restarting the sequence for one starts or restarts the sequence for the other. Some IDL routines use the random number generator, so using them will initialize the seed sequence. An example of such a routine is CLUST_WTS.
Note: Do not alter the seed value returned by this function. The only valid use for the seed argument is to pass it back to a subsequent call. Changing the value of the seed will corrupt the random sequence.
Either an array or a series of scalar expressions specifying the dimensions of the result. If a single argument is specified, it can be either a scalar expression or an array of up to eight elements. If multiple arguments are specified, they must all be scalar expressions. Up to eight dimensions can be specified. If no dimensions are specified, RANDOMU returns a scalar result
The formulas for the binomial, gamma, and Poisson distributions are from Section 7.3 of Numerical Recipes in C: The Art of Scientific Computing (Second Edition), published by Cambridge University Press.
Set this keyword to a 2-element array, [n, p], to generate random deviates from a binomial distribution. If an event occurs with probability p, with n trials, then the number of times it occurs has a binomial distribution.
Note: For n > 1.0 x 107, you should set the DOUBLE keyword.
Set this keyword to force the computation to be done using double-precision arithmetic.
RANDOMU constructs double-precision uniform random deviates using the formula:
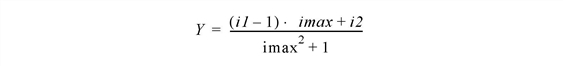
where i1 and i2 are integer random deviates in the range [1...imax], and
imax = 231– 2 is the largest possible integer random deviate. The Y values will be in the range 0 < Y < 1.
Set this keyword to an integer order i > 0 to generate random deviates from a gamma distribution. The gamma distribution is the waiting time to the ith event in a Poisson random process of unit mean. A gamma distribution of order equal to 1 is the same as the exponential distribution.
Note: For GAMMA > 1.0 x 107, you should set the DOUBLE keyword.
Set this keyword to return integer uniform random deviates in the range
[1...231 – 2]. If LONG is set, all other keywords are ignored.
Set this keyword to generate random deviates from a normal distribution.
Set this keyword to the mean number of events occurring during a unit of time. The POISSON keyword returns a random deviate drawn from a Poisson distribution with that mean.
Note: For POISSON > 1.0 x 107, you should set the DOUBLE keyword.
Set this keyword to generate random deviates from a uniform distribution.
This example simulates rolling two dice 10,000 times and plots the distribution of the total using RANDOMU. Enter:
PLOT, HISTOGRAM(FIX(6 * RANDOMU(S, 10000)) + $
FIX(6 * RANDOMU(S, 10000)) + 2)
In the above statement, the expression RANDOMU(S, 10000) is a 10,000-element, floating-point array of random numbers greater than or equal to 0 and less than 1. Multiplying this array by 6 converts the range to 0 ≤Y < 6.
Applying the FIX function yields a 10,000-point integer vector with values from 0 to 5, one less than the numbers on one die. This computation is done twice, once for each die, then 2 is added to obtain a vector from 2 to 12, the total of two dice.
The HISTOGRAM function makes a vector in which each element contains the number of occurrences of dice rolls whose total is equal to the subscript of the element. Finally, this vector is plotted by the PLOT procedure.
An example of reusing a state vector to generate a repeatable sequence:
; Init seed for a repeatable sequence:
seed = 1001L
; Print 1st 5 numbers of sequence:
print,randomu(seed,5)
IDL prints:
0.705884 0.285924 0.231151 0.715447 0.532836
Reuse a state vector:
; Re-init seed to same sequence:
seed = 1001L
; Get 5 number of sequence with 5 calls:
for i=0,4 do print, randomu(seed)
IDL prints:
0.705884
0.285924
0.231151
0.715447
0.532836
|
Original |
Introduced |